©作者|Zane
来源|神州问学
MoE技术的优势在于,在算力有限的情况下,它能够以同样的参数规模大幅减少计算量。尽管在拥有充足算力的前提下,传统稠密模型的性能可能更胜一筹,但MoE模型在实际应用中展现出了极高的效率。相同能力下,MoE模型的推理算力需求比稠密模型低了一个量级,这意味着在保持智能模型性能的同时,企业可以用更少的算力投入获得更大的产出。这种效率的提升,为未来解决算力挑战提供了一条新的路径。随着技术的不断进步,MoE有望成为智能模型发展的关键所在,让“分工的艺术”在人工智能领域绽放新的光彩。
稠密模型(Dense Models): 稠密模型是指那些在训练过程中使用所有参数的模型。在稠密模型中,每个输入都与所有模型参数相互作用。这种模型的特点是参数数量多,计算量大,因此需要较高的计算资源。稠密模型通常更容易训练,因为每个参数都在每个训练步骤中更新。
稀疏模型(Sparse Models): 稀疏模型则是在训练过程中只激活部分参数的模型。在稀疏模型中,每个输入只与模型参数的一个子集相互作用,这样可以显著减少计算量和所需的存储空间。稀疏模型通过某种机制(如门控机制)动态地选择激活哪些参数,从而实现参数的有效利用。
在实际应用中,稀疏模型和稠密模型各有优势。稠密模型因其简单性和普适性而被广泛使用,而稀疏模型则在处理大规模数据和资源受限的情况下表现出其独特的优势。随着模型规模的不断扩大,稀疏模型在高效利用资源、提高计算效率方面的价值越来越受到重视。
MoE模型主要由2个关键的部分组成:
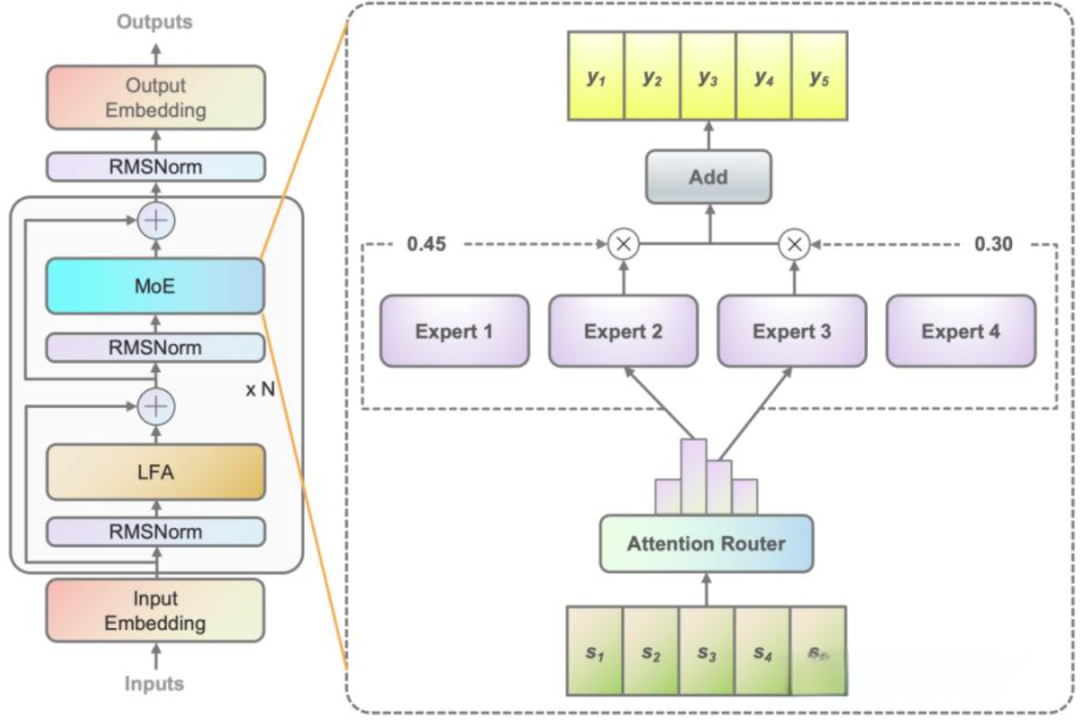
稀疏MoE层:这一部分替代了传统Transformer模型中的前馈网络 (FFN)层。MoE层中包含了若干个“专家”,每个专家都是一个独立的神经网络。在实际应用中,这些专家通常是前馈网络 (FFN),但它们也可以是更复杂的网络结构,甚至可以是 MoE 层本身,从而形成层级式的 MoE 结构。
路由:这个部分用于决定哪些token被发送到哪个“专家”。路由策略有两种:token 选择路由器或路由器选择 token。路由器使用 softmax 门控函数通过专家或 token 对概率分布进行建模,并选择前 k 个。
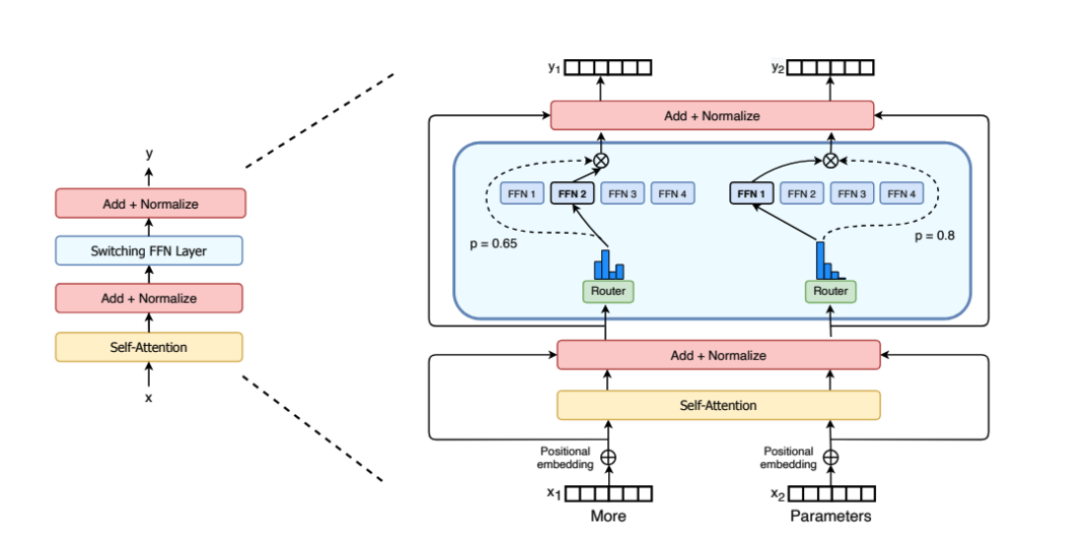
例如,在下图中是Switch Transformers[1]论文中的MoE层,不同的token被发送到不同的专家(FNN)。有时,一个令牌甚至可以被发送到多个专家。令牌的路由是 MoE 使用中的一个关键点,因为路由器由学习的参数组成,并且与网络的其他部分一同进行预训练。
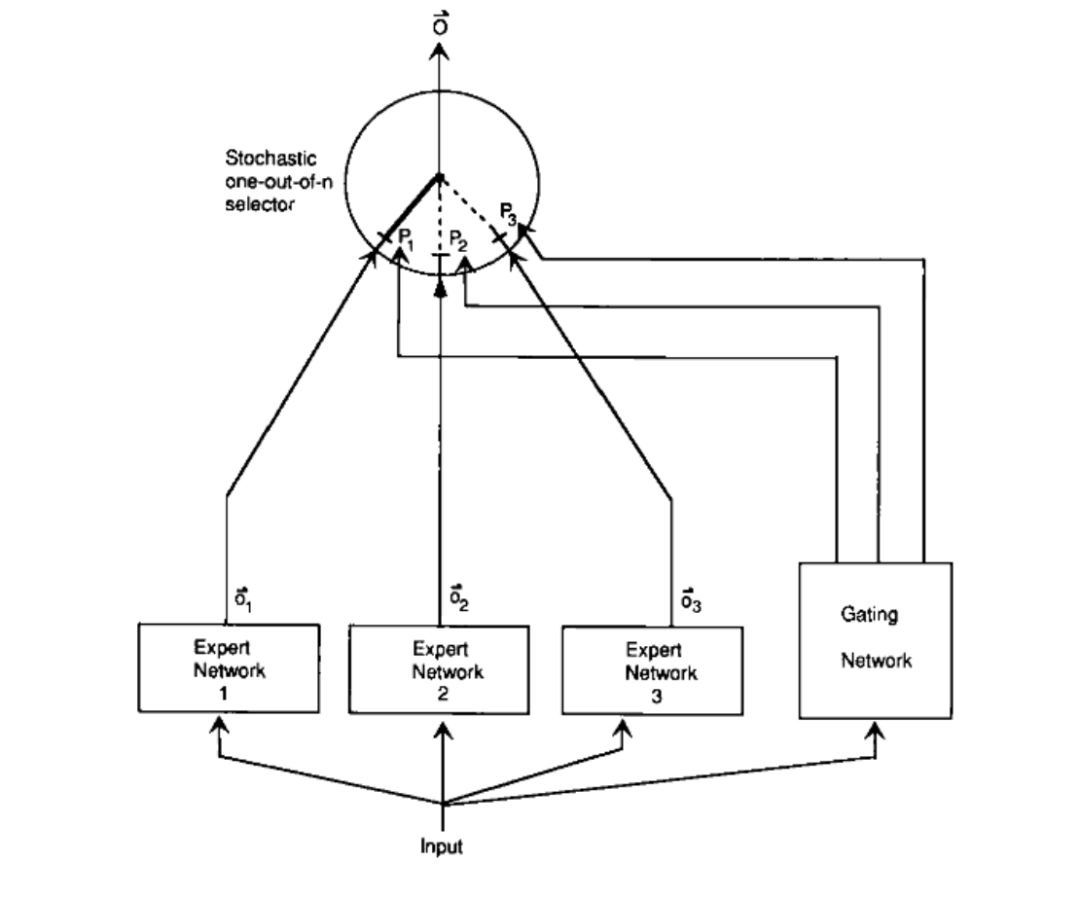
为了减少干扰效应,论文提出了一个创新的方法:构建多个独立的专家系统,每个专家系统负责处理特定场景下的子任务。这样,每个专家可以独立地学习其任务的权重,从而提高了学习效率和模型的泛化能力。
论文中设计了一个基于概率性模型的门控网络,它根据输入数据动态地选择最合适的专家网络来处理当前任务。这种方法使得模型在不同的场景下可以选择不同的专家,就像复仇者联盟中的尼克·弗瑞根据不同的威胁召唤不同的超级英雄一样。
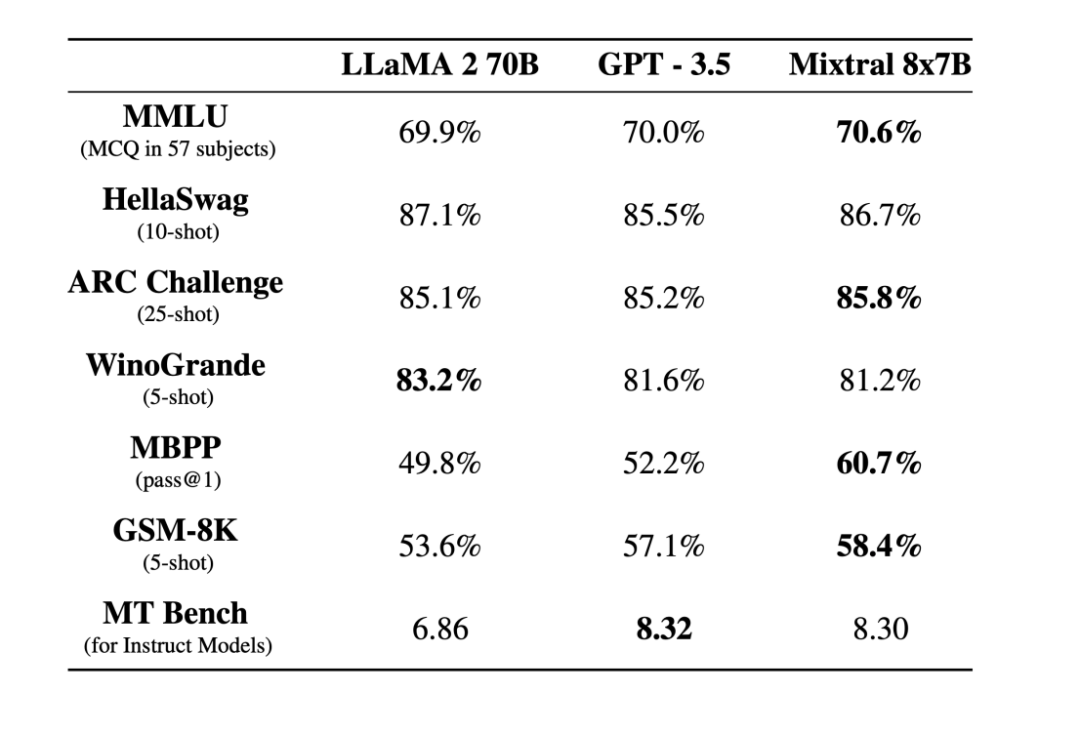
MoE最初作为一种统计学架构提出,随着机器学习和深度学习的发展,它在2017年就已经在LSTM模型上取得了成功应用。最近,随着Mistral AI开源了首个MoE架构模型,MoE在大型模型训练中的应用受到了广泛关注。这一开源项目不仅是对MoE理论的一次成功实践,也标志着MoE从理论研究向实际应用的转变。
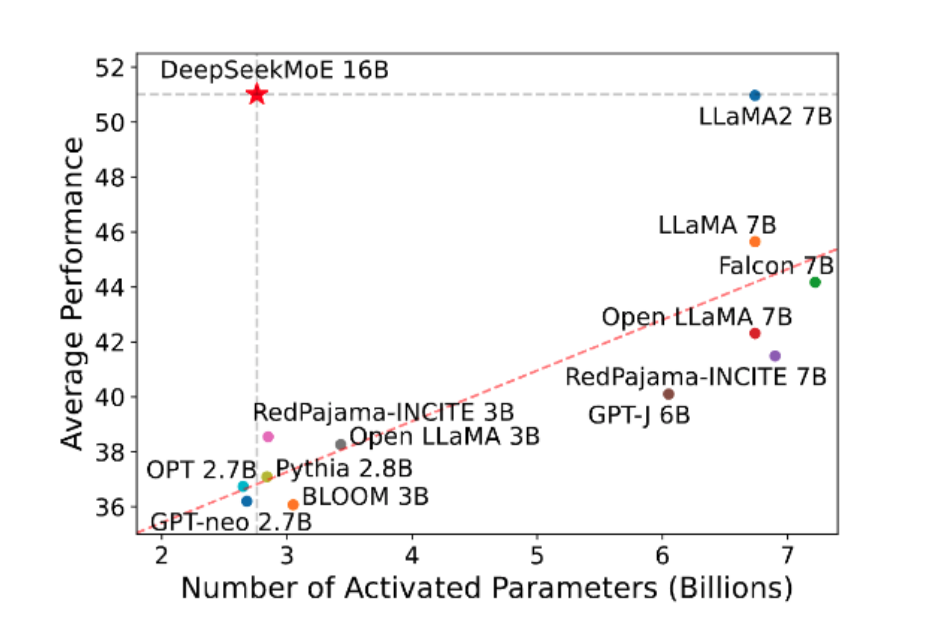
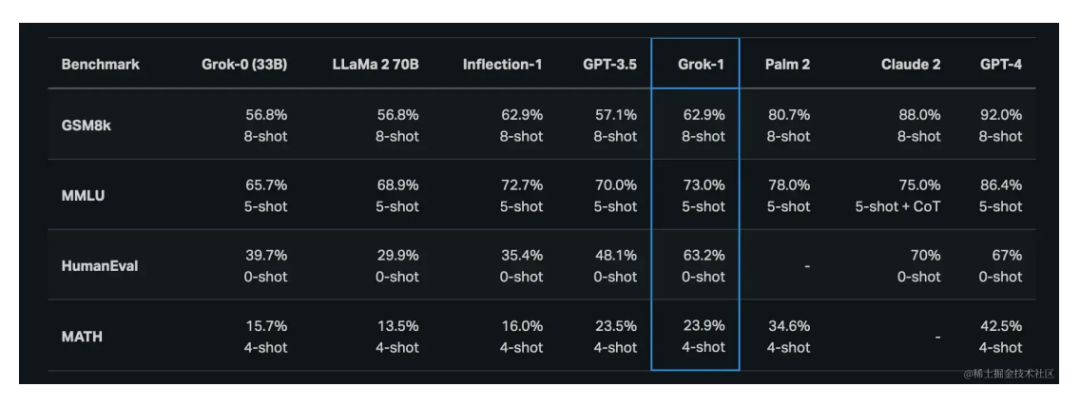
3月28日,Databricks 开源了通用大模型 DBRX,这是一款拥有 1320 亿参数和 360亿 激活参数的混合专家模型(MoE),并支持 32k Tokens 的最长上下文长度。
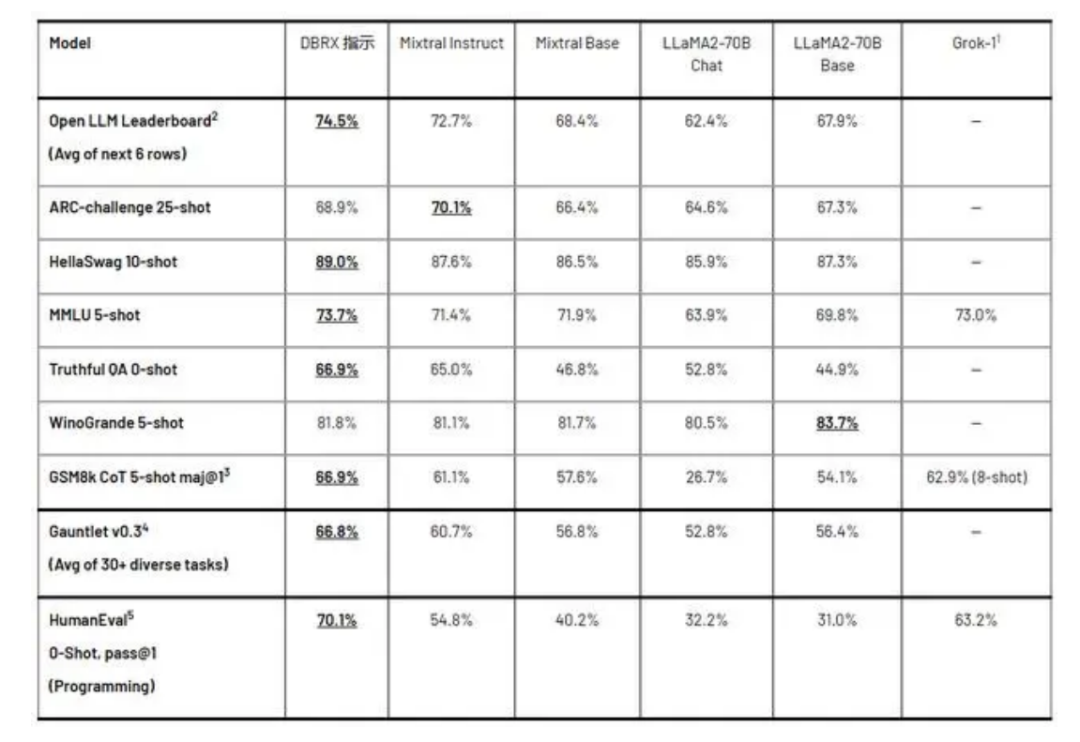
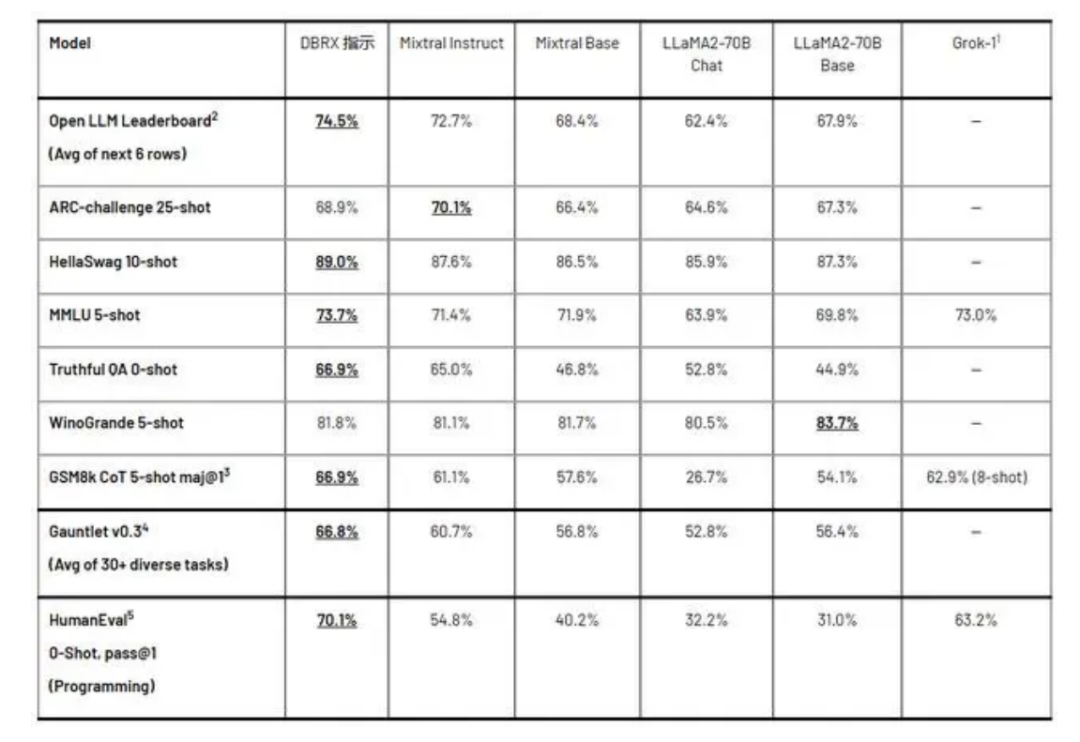
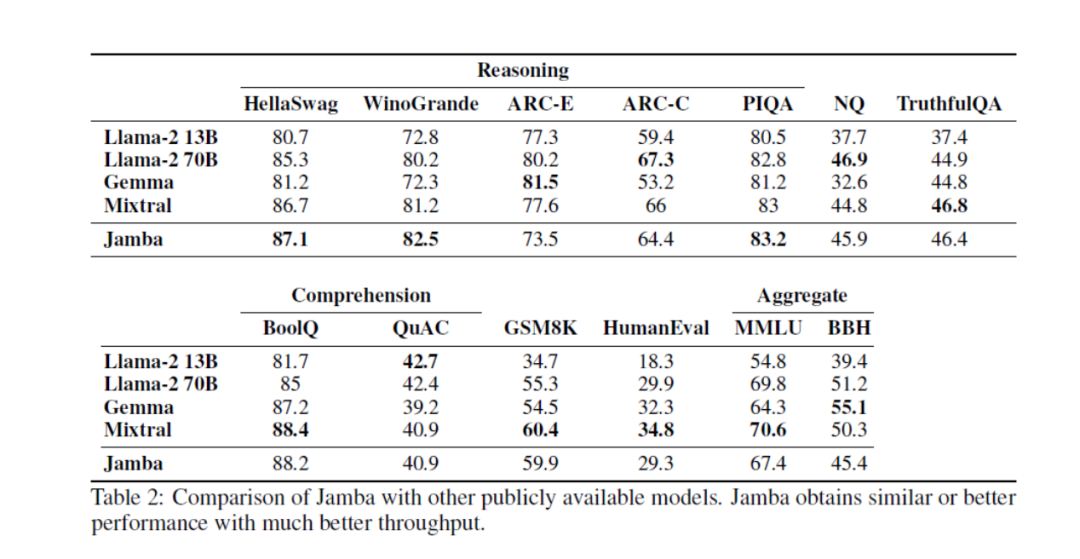
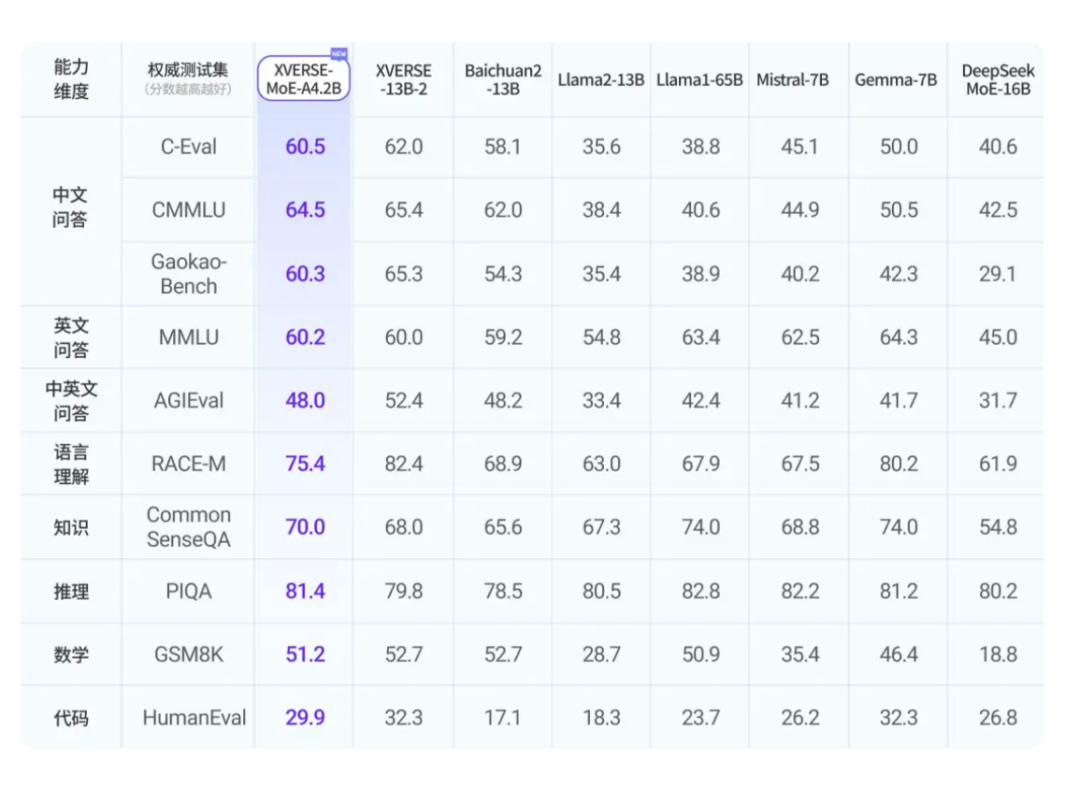
性能提升:MoE有望进一步提高模型的性能,特别是在处理复杂任务和大规模数据集时。通过合理地组合不同专家的能力,MoE可以实现更精细和高效的信息处理。
资源效率:MoE的稀疏性使得模型在训练和推理过程中能够显著减少计算资源的消耗,这对于资源受限的环境尤其有价值。
可扩展性:MoE提供了一种扩展模型规模的新的途径,通过增加专家的数量和多样性,模型可以不断地扩展其能力和覆盖范围。
多任务学习:MoE天然适合于多任务学习场景,因为不同的专家可以专注于不同的任务,而共享的参数可以促进任务间的知识共享。
个性化模型:MoE可以用于构建个性化模型,其中不同的用户或场景可以使用不同的专家组合,以实现更好的个性化服务。
MoE的挑战:
训练难度:MoE模型的训练通常比稠密模型更为复杂,需要精细的动态路由机制和有效的训练策略。
优化算法:目前用于训练MoE的优化算法还不够成熟,需要进一步的研究和开发。
资源分配:如何高效地分配计算资源给不同的专家,以及如何平衡专家之间的负载,是MoE面临的重要挑战。
模型复杂性:随着专家数量的增加,模型的复杂性也会增加,这可能导致过拟合和难以解释的模型行为。
部署挑战:在现实世界中部署MoE模型可能会遇到硬件兼容性和性能优化的挑战。
总的来说,MoE技术为构建高效、大规模的神经网络模型提供了新的思路和方法。尽管面临一些挑战,但随着研究的深入和技术的发展,MoE有望在人工智能领域发挥更大的作用。
当前市面上的MoE模型的一版可以分为2种,一种是从零开始训练,还有一种是基于已有的模型进行训练,比如Mistral 8x7B则是从零训练而来的,而Qwen1.5-MoE则是基于已有的千问模型而来的,对于前者则开销更大,但是却更容易控制训练的内容,最终结果可能更优,而后者则基于已有的模型而来,能够已更快更佳经济的方式得到一个MoE模型,但是因为是基于已有的模型,最终结果可能会受到之前模型的影响较多。
模型微调
目前对于所有的MoE模型来说,整体思路都是一样的基本都是基于transformer架构更换前馈网络层,变成多个“专家”,并在“专家“之上增加一个门控网络,所以对于MoE模型来说,微调则是主要针对这两部分进行。而当前的MoE模型大部分都是基于Transformer模型的所以对于大部分开源的MoE都是可以使用transformer框架进行微调的。
对于MoE模型算法优化&模型复杂度
稠密模型和稀疏模型在过拟合的动态表现上存在显著差异。稀疏模型更易于出现过拟合现象,因此在处理这些模型时,尝试更强的内部正则化措施是有益的,比如使用更高比例的 dropout。例如,我们可以为稠密层设定一个较低的 dropout 率,而为稀疏层设置一个更高的 dropout 率,以此来优化模型性能。
在机器学习中,稠密模型和稀疏模型在对抗过拟合现象方面展现出不同的行为。由于稀疏模型倾向于在参数中保留较少的非零值,它们可能更易受到训练数据中随机噪声的影响,从而增加了过拟合的风险。为了缓解这一问题,对于稀疏模型,采用更为强烈的正则化策略是非常有帮助的,比如应用更高比例的dropout正则化。
例如,在构建神经网络时,我们可以为稠密层选择一个较低的dropout比率,因为这些层通常不会那么容易过拟合。相反,对于稀疏层,由于它们更容易捕捉到数据中的随机波动,我们可以为其分配一个更高的dropout比率,以此来提升模型在未见数据上的表现。
这种策略的核心在于,通过为不同类型的层定制适当的dropout比率,我们可以更有效地平衡模型的复杂性和泛化能力,从而提高整体的模型性能。在实际操作中,这可能需要结合模型的具体结构和数据集的特点,通过反复实验和验证来确定最合适的dropout比率配置。
[2] 《**Adaptive Mixtures of Local Experts**》- Robert A. JacobsMichael I. JordanSteven J. NowlanGeoffrey E. Hinton](https://readpaper.com/paper/2150884987)




